Theorem

The result of the Lemma can be generalized onto a much broader class of Hamiltonian given by (4). Thus let us consider (4) with A and B being peaked functions of $\textbf{q}-\textbf{q}_1$ , which corresponds to waves on a weakly inhomogeneous background. Note that

$$A(\textbf{q}_1,\textbf{q})=A^*(\textbf{q},\textbf{q}_1)$$ (59)

because the Hamiltonian is Hermitian. Moreover

$$B(-\textbf{q},-\textbf{q}_1)=B(\textbf{q}_1,\textbf{q}).$$ (60)

Condition (65) does not really restrict our choice of the coefficient $B(\textbf{q},\textbf{q}_1)$ . Indeed, we can consider any function $B$ and then represent it as a sum of two components

$$B(\textbf{q},\textbf{q}_1)=B^{'}(\textbf{q},\textbf{q}_1)+B^{''}(\textbf{q},\textbf{q}_1),$$ (61)

where

$$B^{'}(\textbf{q},\textbf{q}_1)=\frac{1}{2}(B(\textbf{q},\textbf{q}_1)+B(-\textbf{q}_1,-\textbf{q})),$$

$$B^{''}(\textbf{q},\textbf{q}_1)=\frac{1}{2}(B(\textbf{q},\textbf{q}_1)-B(-\textbf{q}_1,-\textbf{q})),$$

When we plug Eq. (66) into Hamiltonian (4), the part of the integral with $B^{''}$ vanishes.

From now on, we will omit indices wherever it does not lead to a confusion and denote $a\equiv \check{a}_{\textbf{k},\textbf{x}}$ and $a_{-}\equiv \check{a}_{-\textbf{k},\textbf{x}}$ . Also, we introduce some convenient notations, which we will use throughout the rest of the paper. For any function $\varphi(\textbf{k})$ , we denote its even part as $\varphi_{ev}$ and its odd part $\varphi_{od}$

$$\varphi_{ev} = \frac{1}{2}(\varphi+\varphi_{-}),$$

$$\varphi_{od} = \frac{1}{2}(\varphi-\varphi_{-}).$$

We now are ready to formulate the main theorem of this paper:

Theorem 1   Consider a Hamiltonian (4) with $A(\textbf{q},\textbf{q}_1)$ and $B(\textbf{q},\textbf{q}_1)$ being peaked functions of $(\textbf{q}-\textbf{q}_1)$ with the same parameter $\varepsilon$ , i.e., $A(\textbf{q},\textbf{q}_1)=0$ and $B(\textbf{q},\textbf{q}_1)=0$ when $\vert\textbf{q}-\textbf{q}_1\vert>\varepsilon$ . Suppose that conditions (64) and (65) are satisfied. Let us introduce new notations

$$\mu \equiv \int A(\textbf{k}-{\textbf{m}}/2,\textbf{k}+{\textbf{m}}/2) e^{i\textbf{m}\cdot\textbf{x}} d\textbf{m}$$ (62)

$$\lambda \equiv \int B(\textbf{k}-{\textbf{m}}/2,\textbf{k}+{\textbf{m}}/2) e^{i\textbf{m}\cdot\textbf{x}}d\textbf{m}$$ (63)

$$\nu \equiv \Re[\lambda]$$ (64)

$$\widetilde{\nu} \equiv \Im[\lambda]$$

Suppose that Hamiltonian (4) has a dominant diagonal part, i.e. $\mu_{ev}>\nu$ and $\tilde{\nu}=O(\varepsilon)$ . Then, there exists a new-canonical change of variables from $a_\textbf{k}$ to $c_{\textbf{k}\textbf{x}}$ and the evolution of system (4) can be approximately described by the following equation of motion

$$i\frac{\partial}{\partial t}{c_{\textbf{k}\textbf{x}}} = \frac{\delta H_f}{\delta c_{\textbf{k}\textbf{x}}^*},$$

with a filtered Hamiltonian

$$H_f=\int c_{\textbf{k}\textbf{x}}[\omega -\textbf{x}\cdot\nabla_\... ...x}\omega +i\{\omega ,\cdot\}] c_{\textbf{k}\textbf{x}}^*d\textbf{k}d\textbf{x}.$$ (65)

The position dependent frequency is given by the formula

$$\omega=\mu_{od}+\sqrt{\mu_{ev}^2-\nu^2}.$$

The transformation from the Fourier variables $a_\textbf{k}$ to new variables $c_{\textbf{k}\textbf{x}}$ is given in the proof.

Proof. The proof consists of three main steps. In order to diagonalize Hamiltonian (4), we

1. apply the Lemma to simplify the Hamiltonian using the peakness of the kernels,
2. perform Bogolyubov transformation to diagonalize the $O(1)$ part of the Hamiltonian,
3. make a near-identity canonical transformation to diagonalize the $O(\varepsilon )$ part of the Hamiltonian.

Step 1: Applying Lemma.
Similarly to Eq. (26), we can write a filtered Hamiltonian for Eq. (4) as

$$H_f^{(1)} = \int \check{a}(\mu-\textbf{x}\cdot\nabla_\textbf{x}\mu+i\{\mu,\cdot\})\check{a}^*d\textbf{k}d\textbf{x}+$$

$$\frac{1}{2}\int [\check{a}[\lambda-\textbf{x}\cdot\nabla_{\textbf{x}}\lambda+i\{\lambda,\cdot\}]\check{a}_{-}d\textbf{k}d\textbf{x}+c.c.],$$

here, as usual c.c. stands for complex conjugate. From property (65) and definition (68) it follows that $\lambda(-\textbf{k},\textbf{x})=\lambda(\textbf{k},\textbf{x})$ .
Step 2: Bogolyubov transformation.
In this step we apply the usual Bogolyubov transformation. Before doing that notice that Hamiltonian (71) consists of two parts

$$H_f^{(1)}=H_{f,1}^{(1)}+H_{f,\varepsilon }^{(1)},$$

where

$$H_{f,1}^{(1)} = \int\mu \vert\check{a}\vert^2d\textbf{k}d\textbf{x}+\frac{1}{2} \int \nu [\check{a}\check{a}_-+\check{a}^*\check{a}_-^*]d\textbf{k}d\textbf{x},$$

$$H_{f,\varepsilon }^{(1)} = H_f^{(1)}-H_{f,1}^{(1)},$$

are correspondingly $O(1)$ and $O(\varepsilon )$ parts of $H_f^{(1)}$ . In Step 2, we diagonalize the $O(1)$ part using the following linear transformation

$$\check{a}=u_{\textbf{k}\textbf{x}}b + v_{\textbf{k}\textbf{x}}b^*_-.$$ (66)

It was shown in [10] that transformation (73) is canonical if the following conditions are satisfied:

$$\vert u_{\textbf{k}\textbf{x}}\vert^2 - \vert v_{\textbf{k}\textbf{x}}\vert^2 = 1,$$

$$u_{\textbf{k}\textbf{x}} v_{-\textbf{k},\textbf{x}} = u_{-\textbf{k},\textbf{x}} v_{\textbf{k}\textbf{x}}.$$

Let us follow [10] and choose

$$u_{\textbf{k}\textbf{x}}=\cosh(\xi_{\textbf{k}\textbf{x}}),$$ (67)

$$v_{\textbf{k}\textbf{x}}=\sinh(\xi_{\textbf{k}\textbf{x}}),$$ (68)

where $\xi_{\textbf{k}\textbf{x}}$ is real and even, but otherwise arbitrary function. Then under change of variables given by Eq. (73), $H_{f,1}^{(1)}$ becomes

$$H_{f,1}^{(1)} = \int \Big[\mu\cosh^2(\xi)+\mu_-\sinh^2(\xi)+2\nu\sinh(\xi)\cosh(\xi)\Big] \vert b\vert^2d\textbf{k}d\textbf{x}$$

$$+ \frac{1}{2}\int\Big[(\mu+\mu_-)\sinh(\xi)\cosh(\xi)+\nu\big(\cosh^2(\xi)+\sinh^2(\xi)\big)\Big](bb_-+b^*b_-^*)d\textbf{k}d\textbf{x}$$

Denote an expression in square brackets multiplying $\vert b\vert^2$ as $\omega$ :

$$\omega = \Big[\mu\cosh^2(\xi)+\mu_-\sinh^2(\xi)+ 2\nu\sinh(\xi)\cosh(\xi)\Big].$$

Using trigonometric formulas for hyperbolic functions, we obtain

$$\omega =\mu_{ev}\cosh(2\xi)+\mu_{od}+\nu\sinh(2\xi).$$ (69)

In order to diagonalize $H_{f,1}^{(1)}$ , we require that the following condition in satisfied

$$\mu_{ev}\sinh(\xi)\cosh(\xi)+\nu\Big(\cosh^2(\xi)+\sinh^2(\xi)\Big)=0.$$ (70)

This condition is equivalent to

$$\tanh(2\xi)=-\frac{\nu}{\mu_{ev}}.$$ (71)

Since $\mu_{ev}>\nu$ , we can choose $\cosh(2\xi)$ to be positive and, therefore, we have

$$\cosh(2\xi) = \frac{\mu_{ev}}{\sqrt{\mu_{ev}^2-\nu^2}},$$ (72)

$$\sinh(2\xi) = -\frac{\nu}{\sqrt{\mu_{ev}^2-\nu^2}}.$$ (73)

In Appendix B, we find the expression for $\xi$ . Resolving Eq. (76) together with Eqs. (79) and (80), we obtain

$$\omega = \omega_{ev}+ \omega_{od},$$

$$\omega_{od} = \mu_{od},$$

$$\omega_{ev} = \sqrt {\mu_{ev}^2-\nu^2}.$$

Therefore, we have diagonalized $H_{f,1}^{(1)}$ to the form

$$H_{f,1}^{(1)}=\int b\omega b^*d\textbf{k}d\textbf{x}.$$ (74)

Next, we consider the $O(\varepsilon )$ part of the filtered Hamiltonian. In Appendix C, we show that Bogolyubov transformation (73) transforms $H_{f,\varepsilon }^{(1)}$ to the form

$$H_{f,\varepsilon }^{(1)} = \int b\big(-\textbf{x}\cdot\nabla_{\textbf{x}}\omega +i\{\omega ,... ...\mu_{ev}^2}{2\nu}b\left\{\varphi,b_-\right\}+c.c.\right)d\textbf{k}d\textbf{x},$$

where

$$\sigma = \frac{\mu_{ev}^2}{2\nu}\left(\textbf{x}\cdot\nabla_{\textbf{x}}\f... ...a_{ev}}{\mu_{ev}}\right)+\frac{i}{2}\{\mu_{od},\xi\}+\frac{i}{2}\widetilde{\nu}$$

$$\varphi = \sqrt{1-\frac{\nu^2}{\mu_{ev}^2}}=\frac{\omega_{ev}}{\mu_{ev}}$$

Combining Eqs. (81) and (82), we finally obtain Hamiltonian in the form

$$H_f^{\varepsilon } = \int b\big(\omega -\textbf{x}\cdot\nabla_{\textbf{x}}\omega+i\{\o... ...\mu_{ev}^2}{2\nu}b\left\{\varphi,b_-\right\}+c.c.\right)d\textbf{k}d\textbf{x}.$$ (75)

Step 3: Near-identity transformation.
In Step 2, we diagonalized $O(1)$ part but not all of the $O(\varepsilon )$ part. In order to diagonalize complete Hamiltonian, we use the near-identity transformation. This near-identity transformation changes variables from $b_{\textbf{k}\textbf{x}}$ to $c_{\textbf{k}\textbf{x}}$ by the following rule

$$b_{\textbf{k}\textbf{x}}=c_{\textbf{k}\textbf{x}}+\alpha _\textbf... ...tbf{x}}^*+\beta _\textbf{k}\{\gamma _\textbf{k},c_{-\textbf{k},\textbf{x}}^*\},$$ (76)

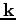
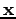
where, we assume that $\beta _\textbf{k}$ and $\gamma _\textbf{k}$ are $O(1)$ terms and $\alpha _\textbf{k}$ and $\big(\beta _\textbf{k}\{\gamma _\textbf{k},c_{-\textbf{k}}^*\}\big)$ are $O(\varepsilon )$ which makes our transformation indeed near identical. Note that $\alpha _\textbf{k}$ , $\beta _\textbf{k}$ , and $\gamma _\textbf{k}$ are functions of both $\textbf{k}$ and $\textbf{x}$ . 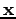Nevertheless, for simplicity of notation, we do omit the dependence on $\textbf{x}$ , since it would only unnecessarily pollute the notations. In Appendix D, we derive the canonicity conditions for transformation (84). In turns out that transformation (84) is canonical if the following conditions are met

$$\beta _\textbf{k} = \beta _{-\textbf{k}},$$

$$\gamma _\textbf{k} = \gamma _{-\textbf{k}},$$

$$\alpha_{od} = \frac{1}{2}\{\gamma _\textbf{k},\beta _\textbf{k}\}.$$

Among the coefficients $\alpha _\textbf{k}$ , $\beta _\textbf{k}$ and $\gamma _\textbf{k}$ that satisfy the canonicity conditions we have to choose those that will diagonalize the $O(\varepsilon )$ part. In Appendix E, we show that such coefficients become

$$\alpha _\textbf{k} = -\frac{\sigma_\textbf{k}^*}{\omega_{ev}}-\frac{\beta _\textbf{k}}{2\omega_{ev}}\left\{\omega_{od},\frac{\omega _{ev}}{\mu_{ev}}\right\},$$

$$\beta _\textbf{k} = \frac{i\mu_{ev}^2}{2\nu\omega_{ev}},$$

$$\gamma _\textbf{k} = \frac{\omega_{ev}}{\mu_{ev}}.$$

Note that these conditions are in full correspondence with the canonicity conditions (85). The Hamiltonian in new variables up to $O(\varepsilon )$ order is

$$H_f=\int c[\omega -\textbf{x}\cdot\nabla_\textbf{x}\omega +i\{\omega ,\cdot\}]c^*d\textbf{k}d\textbf{x}$$

This completes the proof of the main result of this paper. $\qedsymbol$