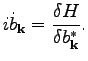Canonicity conditions for near-identity transformation

Here, we obtain the canonicity conditions for the coefficients of the near-identity transformation (84). For the canonicity up to $O(\varepsilon )$ order, we use the equation of motion in the Hamiltonian form.

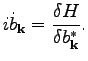$$i\dot{b}_\textbf{k}=\frac{\delta H}{\delta b_\textbf{k}^*}.$$ (99)

In this Appendix for simplicity of notation, we skip writing 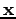$\textbf{x}$ in the subscript of the dynamical variables. Using Eq. (84), we obtain

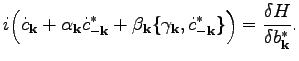$$i\Big(\dot{c}_\textbf{k}+\alpha _\textbf{k}\dot{c}_{-\textbf{k}}^... ...extbf{k},\dot{c}_{-\textbf{k}}^*\}\Big)=\frac{\delta H}{\delta b_\textbf{k}^*}.$$ (100)

Since we are neglecting terms of the order higher than $O(\varepsilon )$ , we can use the following approximation

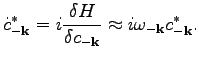$$\dot{c}_{-\textbf{k}}^*=i\frac{\delta H}{\delta c_{-\textbf{k}}}\approx i\omega_{-\textbf{k}}c_{-\textbf{k}}^*.$$ (101)

Combining Eqs. (110) and (111), we obtain

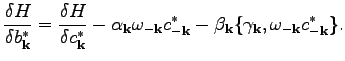$$\frac{\delta H}{\delta b_\textbf{k}^*}=\frac{\delta H}{\delta c_\... ...\beta _\textbf{k}\{\gamma _\textbf{k},\omega _{-\textbf{k}}c_{-\textbf{k}}^*\}.$$ (102)

Further, we have the chain rule in the form

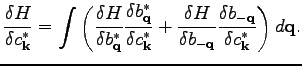$$\frac{\delta H}{\delta c_\textbf{k}^*}=\int\left(\frac{\delta H}{... ...bf{q}}} \frac{\delta b_{-\textbf{q}}}{\delta c_\textbf{k}^*}\right)d\textbf{q}.$$ (103)

Using Eq. (84), we find

$$\frac{\delta b_\textbf{q}^*}{\delta c_\textbf{k}^*} = \delta_\textbf{k}^\textbf{q},$$

$$\frac{\delta b_{-\textbf{q}}}{\delta c_\textbf{k}^*} = \alpha_{-\textbf{q}}\delta_\textbf{k}^\textbf{q}-\beta_{-\textbf{q}}\{\gamma_{-\textbf{q}},\delta_\textbf{k}^\textbf{q}\}_\textbf{q},$$

where the subscript of the Poisson bracket indicates the differentiation with respect to $\textbf{q}$ . Therefore, Eq. (113) becomes

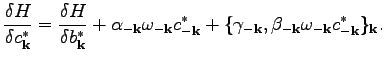$$\frac{\delta H}{\delta c_\textbf{k}^*}=\frac{\delta H}{\delta b_\... ...tbf{k}},\beta_{-\textbf{k}}\omega _{-\textbf{k}}c_{-\textbf{k}}^*\}_\textbf{k}.$$ (104)

Combining Eqs. (112) and (114), we find

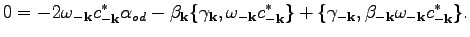$$0=-2\omega _{-\textbf{k}}c_{-\textbf{k}}^*\alpha_{od}-\beta _\tex... ...ma _{-\textbf{k}},\beta _{-\textbf{k}}\omega _{-\textbf{k}}c_{-\textbf{k}}^*\}.$$ (105)

Finally, we obtain the canonicity conditions given in Eq. (85).