


Next: Canonicity conditions for near-identity
Up: Canonical Hamiltonians for waves
Previous: Calculation of
Bogolyubov transformation of the
 part
part
Here, we show how Bogolyubov transformation works on
 .
We consider the terms of Eq. (72) starting with
.
We consider the terms of Eq. (72) starting with
Here we used the following equalities
Next, we consider the terms of Eq. (72) with the Poisson bracket
| |
|
 |
|
| |
|
 |
(94) |
Note that
 terms give zero because their coefficients are purely imaginary and we add c.c. values in the end,
terms give zero because their coefficients are purely imaginary and we add c.c. values in the end,
-
 terms can be obtained as c.c. of
terms can be obtained as c.c. of
 terms.
terms.
Here,  denotes a gradient either with respect to
denotes a gradient either with respect to
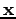 or with respect to
or with respect to
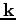 .
Now, let us consider (104) term by term.
.
Now, let us consider (104) term by term.
-
 and
and
 :
:
| |
|
![$\displaystyle \frac{i}{2}\int \left[u^2b\{\mu,b^*\}+\underbrace{v^2b_-^*\{\mu,b...
...f{k}\rightarrow-\textbf{k}$}}
+uvb\{\nu,b^*\}\right]d\textbf{x}d\textbf{k}+c.c.$](img449.png) |
|
| |
|
 |
(95) |
Here, we used the fact that

 and
and  :
:
Here, we have used Eq. (101).
-
 and
and
 :
:
We used Eq. (103) here.
Finally, the rest of
 terms are
terms are
 |
|
|
(98) |
Combining Eqs. (102), (105), (106), (107), and (108), we obtain the
 part of the Hamiltonian given by
Eq. (83).
part of the Hamiltonian given by
Eq. (83).



Next: Canonicity conditions for near-identity
Up: Canonical Hamiltonians for waves
Previous: Calculation of
Dr Yuri V Lvov
2008-07-08