


Next: Bibliography
Up: Canonical Hamiltonians for waves
Previous: Canonicity conditions for near-identity
Near-identity transformation
Lets us first apply the near-identity transformation to the  part of the Hamiltonian that is given by Eq. (81)
part of the Hamiltonian that is given by Eq. (81)
To apply this transformation to the
 part we just need to substitute
part we just need to substitute  with
with  in Eq. (82).
The non-diagonal terms cancel in the Hamiltonian if
in Eq. (82).
The non-diagonal terms cancel in the Hamiltonian if
 |
|
|
(106) |
Let us choose
 |
|
|
(107) |
Then we can rewrite Eq. (116) as
Integrating by parts one can show that
Therefore, the diagonalizing condition becomes
From Eq. (118), the condition on  immediately follows
immediately follows
 |
|
|
(108) |
In order to obtain the condition on  , we expand the second term in the integral
, we expand the second term in the integral
 |
|
|
(109) |
Integral over the last two terms vanishes because these functions are odd.
Therefore, we consider only the other two terms.
Next, we insert this expansion into Eq. (118)
Then, we obtain the following diagonalizing conditions on 
Let us prove that
 .
Substituting Eq. (118) into Eq. (121), we obtain
.
Substituting Eq. (118) into Eq. (121), we obtain
Expanding the Poisson bracket we find the following identity
 |
|
|
(112) |
According to the definition,
 .
Differentiation of both sides of the last equality with respect to
.
Differentiation of both sides of the last equality with respect to
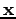 or
or
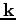 yields
yields
 |
|
|
(113) |
We use Eq. (123) to show that
Plugging Eq. (124) into Eq. (122) proves that
 .
.



Next: Bibliography
Up: Canonical Hamiltonians for waves
Previous: Canonicity conditions for near-identity
Dr Yuri V Lvov
2008-07-08





