next up previous
Next: Estimation of the two-loop Up: Statistical Description of Acoustic Previous: Rules for writing and

Calculation of $\Sigma ({\bf k},\omega )$ -details

Let us start from (4.18) and introduce $\Sigma({\bf k})=\Sigma({\bf k},\omega_*)$ with $\omega_*$ given by (4.14):
    $\displaystyle \Sigma({\bf k})= \int \frac{d^3 k_1 d^3 k_2}{(2\pi)^3}$ (112)
  $\textstyle \times$ $\displaystyle \Bigg( \frac{\vert V({\bf k}_2,{\bf k},{\bf k}_1)\vert^2 \delta({... ..._2)\big]} {\omega({\bf k})+\omega({\bf k}_1) -\omega({\bf k}_2)+i\Gamma_{k12} }$  
  $\textstyle +$ $\displaystyle \frac{\vert V({\bf k}_0,{\bf k}_1,{\bf k}_2)\vert^2 \delta({\bf k... ..._2)} {\omega({\bf k})-\omega({\bf k}_1)-\omega({\bf k}_2)+i\Gamma_{k12} }\Bigg)$  

where
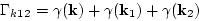\begin{displaymath} \Gamma_{k12}= \gamma({\bf k})+ \gamma({\bf k}_1)+ \gamma({\bf k}_2) \end{displaymath} (113)

is ``triad-interaction'' frequency and $1/\Gamma_{k12}$ is triad interaction time. One can consider (B1 - B2) as an integral equation for the damping of wave $ \gamma({\bf k})=-{\rm Im}\Sigma({\bf k})$ and for the frequency $\omega({\bf k})=\omega_0({\bf k})+{\rm Re}\Sigma({\bf k})$.

First we consider these equations in the limit of weak interaction where, $\Gamma\to 0$, and the main contribution to the first term in (B1) comes from the region where

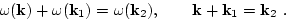\begin{displaymath} \omega({\bf k})+\omega({\bf k}_1)=\omega({\bf k}_2), \qquad {\bf k}+{\bf k}_1={\bf k}_2 \ . \end{displaymath} (114)

These are conservation laws for 3-wave confluence processes $0+1\to 2$. The main contribution for the second term in (B1) comes from the region
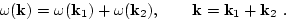\begin{displaymath} \omega({\bf k})=\omega({\bf k}_1)+\omega({\bf k}_2), \qquad {\bf k}={\bf k}_1+{\bf k}_2 \ . \end{displaymath} (115)

These are conservation laws for decays processes $0\to 1+2$. For weak interaction one may replace in (4.2) and (4.3) $\ \ \omega({\bf k})$ on $\omega_0({\bf k}) = c k$. Than it follows from (4.2) and (4.3) that ${\bf k}_1 \parallel {\bf k}_2 \parallel {\bf k}$ with ${\bf k}_1,{\bf k}_2$ directed along ${\bf k}$. This fact makes it natural to introduce in integrals (B1) new variables: scale positive variable $q>0$ and two-dimensional vector $\bf\kappa$ such that
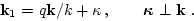\begin{displaymath} {\bf k}_1=q {\bf k} /k +{\bf\kappa }\,, \qquad {\bbox \kappa }\perp{\bf k}\ . \ \end{displaymath} (116)

In the first term of (B1)
\begin{displaymath}{\bf k}_2=(k+q){\bf k} /k +{\bf\kappa }, \qquad 0\le q \ . \end{displaymath} (117)

In the second term
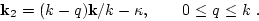\begin{displaymath}{\bf k}_2=(k-q){\bf k} /k -{\bf\kappa }, \qquad 0\le q\le k \ . \end{displaymath} (118)

For $\kappa\ll k$ the denominators in integrals (B1) strongly depend on $\kappa$. Indeed:
$\displaystyle \omega_0({\bf k})+\omega({\bf k}_1)-\omega(\vert{\bf k}+{\bf k}_1\vert)$ $\textstyle =$ $\displaystyle c k \frac{\kappa^2}{2q(k+q)}\,,$ (119)
$\displaystyle \omega_0({\bf k})-\omega({\bf k}_1)-\omega(\vert{\bf k}-{\bf k}_1\vert)$ $\textstyle =$ $\displaystyle -c k \frac{\kappa^2} {2q(k-q)} \ .$ (120)

This allows to neglect $\kappa$ dependence of interaction $V({\bf k},{\bf q},{\bf p})$ and correlation $n({\bf k}_i)$ in numerator of (B1) for estimation. The result is
$\displaystyle \Sigma({\bf k})$ $\textstyle =$ $\displaystyle \frac{A^2k}{8\pi^2}\int_0^{k^2}d\kappa^2 \Bigg[ \int_0^\infty d q \frac{q(k+q)\big[n(q)-n(k+q)\big]} {c k \kappa^2/[2q(k+q)]+i\Gamma_{k12}}$  
  $\textstyle +$ $\displaystyle \int_o^kd q \frac{q(k-q)n(q)} {-c k \kappa^2/[2q(k-q)]+i\Gamma_{k12}} \Bigg] \ ,$ (121)

where
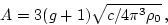\begin{displaymath} A=3(g+1)\sqrt{c/4\pi^3\rho_0}\,, \end{displaymath} (122)

is a factor in (2.20) so that for parallel or almost parallel wavevectors $V({\bf k}, {\bf q},{\bf p}) =A\sqrt{k q p}$. After changing of variables this integral becomes to be more transparent:
    $\displaystyle \Sigma({\bf k})=\frac{A^2}{4\pi^2 c} \Bigg[\int d q \int_0^{y_{\rm max}} d y q^2(k+q)^2$ (123)
  $\textstyle \times$ $\displaystyle \frac{[n(q)-n(k+q)]}{y+i\Gamma_{k12}} -\int_0^{y_{\rm max}} d y\int_o^k d q \frac{q^2(k-q)^2n(q)}{y-i\Gamma_{k12}} \Bigg] \ .$  

One may estimate $y_{\rm max}\simeq c k^2 / 2 q $ from the fact that our expressions were obtained by expanding in $ \kappa / k$, therefore should be at least $\kappa<k$.

Now let us consider the imaginary and real part of $\Sigma$ separately. It is convenient to begin with $ \gamma({\bf k})=-{\rm Im}\Sigma({\bf k})$:

$\displaystyle \gamma({\bf k})$ $\textstyle \simeq$ $\displaystyle \frac{A^2}{4\pi^2 c} \int_0^\infty d y \Bigg[\int_0^\infty d q q^2(k+q)^2\Gamma_{k12}$ (124)
  $\textstyle \times$ $\displaystyle \frac{ \big[n(q)-n(k+q)\big]} {y^2+\Gamma_{k12}^2} + \int_0^k d q \frac{q^2(k-q)^2n(q)\Gamma_{k12}}{y^2+\Gamma^2_{k12}} \Bigg] \ .$  

Here we changed the upper limit of integration: $y_{\rm max}\to\infty$ because the main contribution to the integral comes from the area $y\simeq\Gamma\ll c k$. After trivial integration with respect of $y$ one has:
$\displaystyle \gamma({\bf k})$ $\textstyle \simeq$ $\displaystyle \frac{A^2}{8\pi c }\Bigg[ \int_0^\infty q^2(k+q)^2\big[n(q)-n(k+q)\big] d q$  
    $\displaystyle + \int_0^k q^2(k-q)^2n(q) d q\Bigg] \ .$ (125)

This expression for $ \gamma({\bf k})$ corresponds to that given by the kinetic equation [1] for waves. For further progress it is necessary to do some assumption about $n(q)$. Let us assume that $n(q)$ vanishes with growing of $q$ faster than $1/q^4$.[*] For such spectra the main contribution to the integral comes from small $q\ll k$. In this case contributions from first and second integrals in (B14) coincides and may be represented in the form:
$\displaystyle \gamma(k)=\frac{A^2 k^2}{4 \pi c }\int_{1/L}^\infty {n(q) q^2 d q} \simeq \frac{A^2 k^2 }{4\pi c } N(\Omega) \ .$     (126)

In this case contributions from first and second integrals in (B14) coincides and may be represented in the form:
$\displaystyle \gamma(k)=\frac{A^2 k^2}{4 \pi c }\int_{1/L}^\infty {n(q) q^2 d q} \simeq \frac{A^2 k^2 }{4\pi c } N(\Omega) \ .$     (127)

next up previous
Next: Estimation of the two-loop Up: Statistical Description of Acoustic Previous: Rules for writing and
Dr Yuri V Lvov 2007-01-17