Next: Bibliography Up: Statistical Description of Acoustic Previous: Calculation of -details

Estimation of the two-loop diagrams.

Let us write down analytical expression which correspond to one of the diagrams (b) in Fig.1(b)

$\displaystyle \Sigma_b({\bf k},\omega)$	$\displaystyle = \int \frac{ d{\bf k_1} d {\bf k_2} d\omega_1 d\omega_2} {(2\pi)^8} V_a V_b V_c V_d n(k_1,\omega_1)n(k_2,\omega_2)$
	$\displaystyle \times G({\bf k_1}+{\bf k_2}, \omega_1+\omega_2) G({\bf k}+{\bf k_1}+ {\bf k_2},\omega+\omega_1+\omega_2)$
	$\displaystyle \times G({\bf k}+{\bf k},\omega+\omega_2)$	(128)

where

are vertices,

$\displaystyle V_a=V({\bf k_1}+{\bf k_2}+{\bf k},{\bf k},{\bf k_1}+{\bf k_2}),$			(129)
$\displaystyle V_b=V({\bf k_1}+{\bf k_2}+{\bf k},{\bf k_1},{\bf k}+{\bf k_2}),$			(130)
$\displaystyle V_c=V({\bf k_2}+{\bf k},{\bf k_2},{\bf k}),$			(131)
$\displaystyle V_d=V({\bf k_1}+{\bf k_2},{\bf k_1},{\bf k_2})$			(132)

We just followed the rules of DT and integrated over all delta-functions. From now, the analyses will be parallel to that of appendix B. Let us use (4.16) for $n(k,\omega)$ and (4.11) for $G(k,\omega)$ . Now we can easily perform integration over $\omega_1$ and $\omega_2$ . Now, as it was done in appendix B, introduce $\Sigma_b({\bf k})=\Sigma_b({\bf k},\omega_*)$ . Since all interacting wavevectors are almost parallel, we introduce two-dimensional vectors $\bf\kappa_1$ and $\bf\kappa_2$ such that

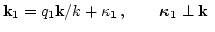$\displaystyle {\bf k}_1=q_1 {\bf k} /k +{\bf\kappa_1 }\,, \qquad {\bbox \kappa_1 }\perp{\bf k}\$			(133)
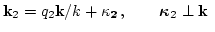$\displaystyle {\bf k}_2=q_2 {\bf k} /k +{\bf\kappa_2 }\,, \qquad {\bbox \kappa_2 }\perp{\bf k}\$			(134)

We use $V({\bf k}, {\bf q},{\bf p}) =A\sqrt{k q p}$ . Since $\kappa_i\ll k$ , we can expand resonance denominators in (C1) with respect to $\kappa_i$ . The integrals will be dominated by regions, where $q_i\ll k$ . By putting everything together, one gets

$\displaystyle \Sigma_b({\bf k})\simeq \int \frac{ \pi^2 d q_1 d q_2 d \kappa_1^2 d \kappa_2^2}{2\pi^6} A^4 k^3 (q_1+q_2) q_1 q_2 \tilde n_{q_1} \tilde n_{q_2}$			(135)
$\displaystyle \left[ (\frac{c(\kappa_1^2+\kappa_2^2)}{2(q_1+q_2)}+ \Gamma_{q_1,... ... (\frac{c}{2} \frac{\kappa_1^2}{q_1}+\frac{\kappa_2^2}{q_2} +i\gamma_k) \right.$
$\displaystyle \left. (\frac{c \kappa_2^2}{2 q_2}+ i \gamma_k)\right]^{-1}$			(136)

Substituting $\tilde n_q=n/q^{-9/2}$ we see, that indeed, the dominant part comes from the region of small

. We can estimate all these integrals to get

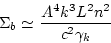$\begin{displaymath}\Sigma_b\simeq \frac{A^4 k^3 L^2 n^2}{c^2 \gamma_k} \end{displaymath}$

(137)

where we used the small

cutoff

. Finally

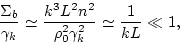$\begin{displaymath} \frac{\Sigma_b}{\gamma_k}\simeq \frac{k^3 L^2 n^2}{\rho_0^2 \gamma_k^2} \simeq\frac{1}{k L}\ll 1, \end{displaymath}$

(138)

and we conclude, that contribution from diagrams of type (b) on Fig.1(b) is much less, than contribution from one-loop diagrams. But this is not the end of the story. Let us try to estimate contributions from diagrams of type (e) on Fig.1(b). Following the same guidelines, we obtain

$\displaystyle \Sigma_e({\bf k})=$		$\displaystyle \int {\frac{d {\bf k_1} {\bf k_2}}{(2 \pi)^8} A^4 k k_1 k_2 (k+k_1) (k+k_1+k_2)(k+k_2) \tilde n_{k_1} \tilde n_{k_2}}$
		$\displaystyle \times \left[ (\omega_k+\omega_{k_1} -\omega_{k+k_1} + i\Gamma_{k,k_1,k+k_1}) \right.$
		$\displaystyle \left.\times (\omega_k+\omega_{k_1}+\omega_{k_2} -\omega_{k+k_1+k_2} + i\Gamma_{k,k_1,k_2,k+k_1+k_2}) \right.$
		$\displaystyle \times\left. (\omega_k+\omega_{k_2} -\omega_{k+k_2} + i\Gamma_{k,k_1,k+k_2})\right]^{-1}$

Let us again introduce $\kappa_1$ and $\kappa_2$ as above, and substituting $\tilde n_q=n/q^{-9/2}$ we obtain the following estimation:

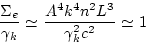$\begin{displaymath}\frac{\Sigma_e}{\gamma_k}\simeq \frac{A^4 k^4 n^2 L^3}{\gamma_k^2 c^2 }\simeq 1 \end{displaymath}$

(139)

Therefore we conclude, that contribution from two loop diagrams is dominated by planar diagrams and of the order of one loop diagrams contribution.

Next: Bibliography Up: Statistical Description of Acoustic Previous: Calculation of -details

Dr Yuri V Lvov 2007-01-17