


Next: Canonical Equation of Motion
Up: Hamiltonian Description of Acoustic
Previous: Equations of Motion and
Let us expand the Hamiltonian (2.11)
(expressed in terms of  ) in power series:
) in power series:
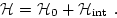 |
(39) |
Here  is quadratic in
is quadratic in  and
and  , giving the
Hamiltonian of non-interacting waves:
, giving the
Hamiltonian of non-interacting waves:
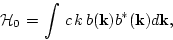 |
(40) |
with linear dispersion relation
 . In the
Hamiltonian of interaction
. In the
Hamiltonian of interaction
 we take into account
only three-wave processes:
we take into account
only three-wave processes:
We neglected here
 processes (processes described
by
processes (processes described
by
 and
and  terms), because they are
nonresonant. It means, that if we take into account
terms), because they are
nonresonant. It means, that if we take into account
 term, it is not going to change our final results,
thus we can neglect it from the very beginning. We also neglected
contributions from 4-wave and higher terms, because three-wave
interaction is the dominant one.
term, it is not going to change our final results,
thus we can neglect it from the very beginning. We also neglected
contributions from 4-wave and higher terms, because three-wave
interaction is the dominant one.
The coupling coefficient of the 3-wave interaction a given by [1]
where  is some dimensionless constant of the order of unity and
is some dimensionless constant of the order of unity and
 is the angle between
is the angle between  and
and  .
Since we have almost linear dispersion relation, only almost parallel
wavevectors can interact, therefore
.
Since we have almost linear dispersion relation, only almost parallel
wavevectors can interact, therefore
 with the high
accuracy can be replaced by
with the high
accuracy can be replaced by  and (2.20) reduces to
and (2.20) reduces to



Next: Canonical Equation of Motion
Up: Hamiltonian Description of Acoustic
Previous: Equations of Motion and
Dr Yuri V Lvov
2007-01-17