


Next: Evolution of statistics of
Up: Wave Turbulence "Recent developments
Previous: Weak nonlinearity expansion: four-wave
Let us first obtain an asymptotic weak-nonlinearity expansion
for the generating functional
 exploiting the separation of the linear and
nonlinear time scales. 3 To
do this, we have to calculate
exploiting the separation of the linear and
nonlinear time scales. 3 To
do this, we have to calculate  at the intermediate time
at the intermediate time  via
substituting into it
via
substituting into it  from (32)
For the amplitude and phase ``ingredients'' in
from (32)
For the amplitude and phase ``ingredients'' in  we have,
we have,
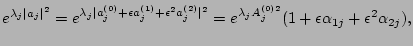 |
(33) |
and
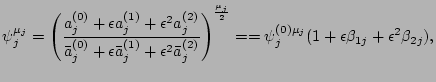 |
(34) |
where
Substituting expansions (39) and (40) into the
expression for  , we have
, we have
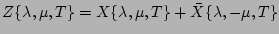 |
(39) |
with
![$\displaystyle X\{\lambda, \mu,T\} = X\{\lambda, \mu,0\} + (2 \pi)^{2N} \left<\p...
...^2}[{\epsilon}J_1 +{\epsilon}^2(J_2 +J_3+J_4+J_5)] \right>_A + O({\epsilon}^4),$](img223.png) |
(40) |
where
where
 and
and
 denote
the averaging over the initial amplitudes and initial phases
(which can be done independently).
Note that so far our calculation for
denote
the averaging over the initial amplitudes and initial phases
(which can be done independently).
Note that so far our calculation for  is the same for the three-wave and
for the four-wave cases. Now we have to substitute expressions for
is the same for the three-wave and
for the four-wave cases. Now we have to substitute expressions for  and
and  which are different for the three-wave and the four-wave cases
and given by
(34), (36) and (34),
(36)
respectively.
which are different for the three-wave and the four-wave cases
and given by
(34), (36) and (34),
(36)
respectively.



Next: Evolution of statistics of
Up: Wave Turbulence "Recent developments
Previous: Weak nonlinearity expansion: four-wave
Dr Yuri V Lvov
2007-01-23
![]() exploiting the separation of the linear and
nonlinear time scales. 3 To
do this, we have to calculate
exploiting the separation of the linear and
nonlinear time scales. 3 To
do this, we have to calculate ![]() at the intermediate time
at the intermediate time ![]() via
substituting into it
via
substituting into it ![]() from (32)
For the amplitude and phase ``ingredients'' in
from (32)
For the amplitude and phase ``ingredients'' in ![]() we have,
we have,


![$\displaystyle \frac{\mu_j}{2A_j^{(0)2}}(a_j^{(2)}\bar
a_j^{(0)}-\bar a_j^{(2)}a...
...
a_j^{(0)}}\right)^2
\right]-\frac{\mu_j^2\vert a_j^{(1)}\vert^2}{4A_j^{(0)2}}.$](img221.png)