


Next: Weakly nonlinear GP equation
Up: Applicability of WKB descriptions
Previous: Strong condensate case
It is interesting that taking the limit of zero condensate amplitude
in the waveaction (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) results in the waveaction
) results in the waveaction
 of the Ehrenfest equation (
of the Ehrenfest equation (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
which corresponds to the regime without condensate,
On the other hand,
)
which corresponds to the regime without condensate,
On the other hand,
 which is
different from the Ehrenfest expression
which is
different from the Ehrenfest expression
 . Thus,
one cannot recover the non-condensate (Ehrenfest) description by just
taking the limit of zero condensate amplitude in (
. Thus,
one cannot recover the non-condensate (Ehrenfest) description by just
taking the limit of zero condensate amplitude in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
(
),
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/share/latex2html/icons/crossref.png) ).
However, one can easily write a unified WKB description which will be
valid with or without condensate by simply adding
).
However, one can easily write a unified WKB description which will be
valid with or without condensate by simply adding  to the
frequency (
to the
frequency (![[*]](file:/usr/share/latex2html/icons/crossref.png) ). Indeed, for strong condensate
). Indeed, for strong condensate
 =const and, therefore, it does not alter the ray equations
(which contain only derivatives of
=const and, therefore, it does not alter the ray equations
(which contain only derivatives of  ). On the other hand, such
an addition allows us to obtain the correct expression
in the limit
). On the other hand, such
an addition allows us to obtain the correct expression
in the limit  . Summarizing, we write the following
equations of the linear WKB theory which are valid with or without the
presence of a condensate,
. Summarizing, we write the following
equations of the linear WKB theory which are valid with or without the
presence of a condensate,
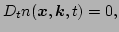 |
(17) |
where
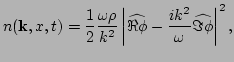 |
(18) |
is the waveaction and
 |
(19) |
is the full time derivative along trajectories and
 |
(20) |
are the ray equations with
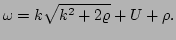 |
(21) |
Formula (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is an important and nontrivial result
which can be obtained neither from existing general facts about the
WBK formalism nor from the linear theory of homogeneous systems.
) is an important and nontrivial result
which can be obtained neither from existing general facts about the
WBK formalism nor from the linear theory of homogeneous systems.



Next: Weakly nonlinear GP equation
Up: Applicability of WKB descriptions
Previous: Strong condensate case
Dr Yuri V Lvov
2007-01-23

