


Next: Applicability of WKB descriptions
Up: Linear dynamics of the
Previous: Linear theory without a
One of the common assumptions in the BEC theory is that the presence
of a condensate acts on the higher levels by just modifying the
confining potential  , see for example [25]. If this was
the case, the linear dynamics would still be described by the
Ehrenfest theorem with some new effective potential. We will show
below that this is not the case.
, see for example [25]. If this was
the case, the linear dynamics would still be described by the
Ehrenfest theorem with some new effective potential. We will show
below that this is not the case.
Let us define the condensate  as a nonlinear coordinate
dependent solution of equation (
as a nonlinear coordinate
dependent solution of equation (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), with a lengthscale of the
order of the ground state size (although it does not need to be
exactly the same as the ground state). In what follows, we will use
Madelung's amplitude-phase representation for
), with a lengthscale of the
order of the ground state size (although it does not need to be
exactly the same as the ground state). In what follows, we will use
Madelung's amplitude-phase representation for  , namely
, namely
 |
(6) |
where
 is the macroscopic speed of the
condensate. It is well known that in this representation
is the macroscopic speed of the
condensate. It is well known that in this representation  obeys
a continuity equation,
obeys
a continuity equation,
 |
(7) |
For future reference, one should note that the second term in this
expression is
 . Thus,
. Thus,  is
is
 too
and it must be neglected in the WKB theory which takes into account
only linear in
too
and it must be neglected in the WKB theory which takes into account
only linear in  terms. We start by considering a small
perturbation
terms. We start by considering a small
perturbation
 , such that
, such that
 |
(8) |
Substituting (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) into (
) into (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we find
) we find
 |
(9) |
where
 is a slowly varying
condensate density.
is a slowly varying
condensate density.
In a similar manner to the previous subsection, the rest of this
derivation consists of Gabor transforming (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), combining the
result with its complex conjugate and finding a suitable waveaction
variable such that the transport equation represents a conservation
equation along the rays. Such a derivation is given in Appendix A. It
yields to the following expression for the waveaction,
), combining the
result with its complex conjugate and finding a suitable waveaction
variable such that the transport equation represents a conservation
equation along the rays. Such a derivation is given in Appendix A. It
yields to the following expression for the waveaction,
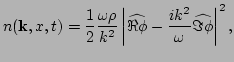 |
(10) |
where  and
and  mean the real and imaginary parts respectively.
As usual, the transport equation takes the form of a conservation
equation for waveaction along the rays,
mean the real and imaginary parts respectively.
As usual, the transport equation takes the form of a conservation
equation for waveaction along the rays,
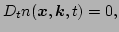 |
(11) |
where
 |
(12) |
is the time derivative along trajectories
 |
(13) |
The frequency is given by the following expression,
 |
(14) |
One can immediately recognize in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) the Bogolubov's
formula [21] which was derived before for systems with
a coordinate independent condensate and without a trapping
potential. It is remarkable that presence of the potential
) the Bogolubov's
formula [21] which was derived before for systems with
a coordinate independent condensate and without a trapping
potential. It is remarkable that presence of the potential  does
not affect the frequency so that expression (
does
not affect the frequency so that expression (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
remains the same. Obviously, the dynamics in this case cannot be
reduced to the Ehrenfest theorem with any shape of potential
)
remains the same. Obviously, the dynamics in this case cannot be
reduced to the Ehrenfest theorem with any shape of potential
 . Therefore, an approach that models a condensate's effect by
introducing a renormalized potential would be misleading in this case.
. Therefore, an approach that models a condensate's effect by
introducing a renormalized potential would be misleading in this case.



Next: Applicability of WKB descriptions
Up: Linear dynamics of the
Previous: Linear theory without a
Dr Yuri V Lvov
2007-01-23
![]() as a nonlinear coordinate
dependent solution of equation (
as a nonlinear coordinate
dependent solution of equation (![]() ), with a lengthscale of the
order of the ground state size (although it does not need to be
exactly the same as the ground state). In what follows, we will use
Madelung's amplitude-phase representation for
), with a lengthscale of the
order of the ground state size (although it does not need to be
exactly the same as the ground state). In what follows, we will use
Madelung's amplitude-phase representation for ![]() , namely
, namely
![]() ), combining the
result with its complex conjugate and finding a suitable waveaction
variable such that the transport equation represents a conservation
equation along the rays. Such a derivation is given in Appendix A. It
yields to the following expression for the waveaction,
), combining the
result with its complex conjugate and finding a suitable waveaction
variable such that the transport equation represents a conservation
equation along the rays. Such a derivation is given in Appendix A. It
yields to the following expression for the waveaction,