Strong condensate case

Now we will consider a strong condensate such that

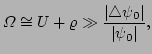$$\Omega \cong U + \varrho \gg \frac{\vert\triangle\psi_{0}\vert}{\vert\psi_{0}\vert},$$ (16)

i.e. the $r$ dependence of the potential $U$ is now balanced by the nonlinearity. This is usually referred to as the Thomas-Fermi limit [6]. Wavepackets now `` feel'' the presence of a strong condensate if $\varrho \sim k^{2}$. We see that the WKB approach is applicable because

$$k^{2}\sim \varrho \gg \frac{1}{r_{0}^{2}} \sim \frac{\vert\triangle\psi_{0}\vert}{\vert\psi_{0}\vert}.$$

According to the ray equations $\omega$ is a constant along a wavepacket's trajectory, so we can find the packet's wavenumber from $k^{2} = \sqrt{\varrho^{2}+\omega^{2}}-\varrho$. One can see that $k^2$ remains positive for any value of $\varrho$ which means that the presence of the condensate does not lead to any new wavepacket reflection points (i.e. when $k$ takes a value of zero). Thus, turbulence is allowed to penetrate into the center of the potential well. However, the group velocity increases when the condensate becomes stronger, $\partial_k \omega \sim \sqrt \rho$. This means that the density of wavepackets decreases toward the center of well. Therefore, the condensate tends to push the turbulence away from the center, toward the edges of the potential trap.

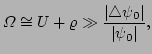
To summarize, in the presence of a strong condensate we have two regions of applicability for our WKB descriptions, see figure 2. Wavepackets at a position $r<r_{0}$, in the central region of the potential well will evolve according to the WKB-condensate description () - (). The Laplacian term only becomes important for $r>r_{0}$ where $\varrho$ is exponentially small. In this case the Ehrenfest description is appropriate. It will be shown in the next section that these two WKB descriptions can be combined into a single set of formulae.