


Next: Appendix B: Hamiltonian formalism
Up: Appendix A: derivation WKB
Previous: The order -
Let us split the wave amplitudes into fastly and
slowly varying parts,
or, in shorthand notation,
where
The  and
and  represent the fastly oscillating parts of
the Gabor transforms. From (
represent the fastly oscillating parts of
the Gabor transforms. From (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) it follows that
) it follows that
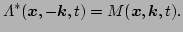 |
(49) |
Obviously,
Our aim now is to derive equations for
 and
and
 . However, due to the relationship (
. However, due to the relationship (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) it is
sufficient to derive an equation for only one of the two, for example
) it is
sufficient to derive an equation for only one of the two, for example
 . From (
. From (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we find
) we find
After substituting our equations for
 and
and
 , (
, (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), and making use of the
relationships (
), and making use of the
relationships (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) the equation for
) the equation for  acquires the
following form:
acquires the
following form:
Here the nonlinear term
 is given by
Note that we have neglected
is given by
Note that we have neglected
 in the above expressions
because, according to the dispersion relationship
(
in the above expressions
because, according to the dispersion relationship
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ), it is of the order of
), it is of the order of  which
is
which
is
 by virtue of (
by virtue of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ). We will also drop
the nonlinear term in the subsequent calculation.
). We will also drop
the nonlinear term in the subsequent calculation.
Our next step is to eliminate the fast oscillations associated with
the Gabor transforms and derive an equation for
 . This
in turn will lead to a natural waveaction quantity which can be used
to describe the behavior of our wavepackets in phase space. Using
(
. This
in turn will lead to a natural waveaction quantity which can be used
to describe the behavior of our wavepackets in phase space. Using
(![[*]](file:/usr/share/latex2html/icons/crossref.png) -
-![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we obtain
) we obtain
Please note that all the terms involving  drop out. This stems from
the fact that, in deriving an equation for
drop out. This stems from
the fact that, in deriving an equation for  , we have had to
divide through by
, we have had to
divide through by  . Therefore, any terms involving
. Therefore, any terms involving  will
result in a factor
will
result in a factor
Thus, after time averaging over a few wave periods,
all the  terms drop out.
terms drop out.
Expanding out equation (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we find the
) we find the  terms cancel
out and using the dispersion relationship (
terms cancel
out and using the dispersion relationship (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we find
) we find
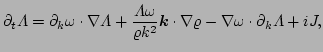 |
(55) |
where
At this point let us drop the nonlinear term and concentrate on the
linear dynamics. Multiplying (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) by
) by
 and
combining it with the complex conjugate equation the
and
combining it with the complex conjugate equation the  terms cancel,
leading to
terms cancel,
leading to
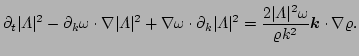 |
(56) |
A similar equation for  can be easily obtained by replacing
can be easily obtained by replacing
 in (
in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and using (
) and using (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
),
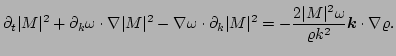 |
(57) |
The LHS of this equation is the full time derivative of  along trajectories. If
along trajectories. If  were to be a correct phase-space
waveaction, the right hand side of this equation would be zero,
however, this is not the case. We find the correct waveaction
were to be a correct phase-space
waveaction, the right hand side of this equation would be zero,
however, this is not the case. We find the correct waveaction
 by setting
by setting
and finding such
 that the the full time
derivative of
that the the full time
derivative of
 is zero. This leads to the
following condition on
is zero. This leads to the
following condition on  ,
,
By choosing
 and substituting it to
(
and substituting it to
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we find
) we find  ,
,  . Therefore the correct form
of the waveaction is
. Therefore the correct form
of the waveaction is
 Summarizing,
we have got the following transport equation for the waveaction
Summarizing,
we have got the following transport equation for the waveaction  in
the linear approximation,
in
the linear approximation,
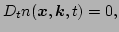 |
(58) |
where
 |
(59) |
is the full time derivative
along trajectories and
 |
(60) |
are the ray equations with
 |
(61) |
Obviously, the dynamics in this case cannot be reduced to the
Ehrenfest theorem with any shape of potential  . Therefore,
approaches that model the condensate effect by introducing a
renormalized potential are misleading.
. Therefore,
approaches that model the condensate effect by introducing a
renormalized potential are misleading.
Finally, it is useful to express the waveaction  in terms of
the original variables,
in terms of
the original variables,
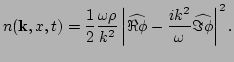 |
(62) |
It is interesting that such a waveaction is in agreement with that found in
[13]. In fact in [13] the homogeneous case with non-zero nonlinearity
(
 ,
,
 ) was considered. This is the opposite limit
to the one we have considered above (where
) was considered. This is the opposite limit
to the one we have considered above (where
 ,
,
 ).
).



Next: Appendix B: Hamiltonian formalism
Up: Appendix A: derivation WKB
Previous: The order -
Dr Yuri V Lvov
2007-01-23
![]() and
and
![]() . However, due to the relationship (
. However, due to the relationship (![]() ) it is
sufficient to derive an equation for only one of the two, for example
) it is
sufficient to derive an equation for only one of the two, for example
![]() . From (
. From (![]() ) we find
) we find

![$\displaystyle = \lambda \left[-\frac{i \nabla\varrho\cdot\nabla\omega}{2k^{2}\v...
...k^{2}\varrho}
- 2\vec{v}
- \frac{i k^{2}\nabla\varrho}{2\omega\varrho}\right]$](img282.png)
![$\displaystyle + \triangle\lambda \left[-\frac{i \omega}{2k^{2}}
-\frac{i k^{2}}{2\omega}\right]
-\frac{k^{2}}{\omega} \nabla\varrho\cdot\partial_{k}\lambda$](img283.png)
![$\displaystyle + \mu \left[\frac{i \nabla\varrho\cdot\nabla\omega}{2k^{2}\varrho...
...la\varrho}{2k^{2}\varrho}
- \frac{i k^{2}\nabla\varrho}{2\omega\varrho}\right]$](img284.png)
![$\displaystyle + \triangle\mu \left[+\frac{i \omega}{2k^{2}}
-\frac{i k^{2}}{2\...
...a}\right]
-\frac{k^{2}}{\omega}\nabla\varrho\cdot\partial_{k}\mu - {\cal{NL}}.$](img285.png)
![$\displaystyle {\cal{NL}}={\cal G} \left[\rho(2 a b + b(a^2+b^2))\right] -\frac{i
k^2}{2\omega_k} {\cal G}\left[( \varrho(3 a^2+b^2+a(a^2+b^2)))\right].$](img287.png)
![]() . This
in turn will lead to a natural waveaction quantity which can be used
to describe the behavior of our wavepackets in phase space. Using
(
. This
in turn will lead to a natural waveaction quantity which can be used
to describe the behavior of our wavepackets in phase space. Using
(![]() -
-![]() ) we obtain
) we obtain
![]() ) we find the
) we find the ![]() terms cancel
out and using the dispersion relationship (
terms cancel
out and using the dispersion relationship (![]() ) we find
) we find

![]() in terms of
the original variables,
in terms of
the original variables,