next up previous
Next: The order - Up: Appendix A: derivation WKB Previous: Appendix A: derivation WKB

The $ \epsilon^0$ order -

As in all WKB based theories we first derive a linear dispersion relationship from the lowest order terms. At zeroth order in $ {\bf \epsilon}$, the spatial derivative of a Gabor transform is $ \nabla\hat{a} = i \vec{k}\hat{a}$ which is similar to the corresponding rule in Fourier calculus. Then, at the lowest order, equations ([*]) and ([*]) become

$\displaystyle \partial_{t}\hat{a}$ $\displaystyle - k^{2} \hat{b} =0,$ (41)
$\displaystyle \partial_{t}\hat{b}$ $\displaystyle + k^{2} \hat{a} + 2\varrho\hat{a} =0.$ (42)

These two linear coupled equations make up an eigenvalue problem. Diagonalizing these equations we obtain

  $\displaystyle \partial_{t}\lambda = +i\omega\lambda,$ $\displaystyle \partial_{t}\mu = -i \omega\mu.$    

Correspondingly, we find the eigenvectors

  $\displaystyle \lambda = \frac{1}{2}\left(\hat{a} - \frac{i k^{2}}{\omega}\hat{b}\right),$ $\displaystyle \mu = \frac{1}{2}\left(\hat{a} + \frac{i k^{2}}{\omega}\hat{b}\right),$ (43)

or, re-arranging for $ \hat{a}$ and $ \hat{b}$

  $\displaystyle \hat{a} = \lambda + \mu,$ $\displaystyle \hat{b} = \frac{i\omega}{k^{2}}(\lambda-\mu).$ (44)

The eigenvalues are given by the dispersion relationship,

$\displaystyle \omega^{2} = k^{2}(k^{2}+2\varrho),$ (45)

which is identical to the famous Bogoliubov form [21] which was also obtained for waves on a homogeneous condensate in the weak turbulence context in [13].

Therefore, at the zeroth order, we see that $ \lambda$ rotates with frequency $ -\omega$ and $ \mu$ rotates at $ +\omega$. Note that the $ \lambda$ and $ \mu$ are related via

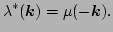$\displaystyle \lambda^{*}(\vec{k}) = \mu (-\vec{k}) .$ (46)

next up previous
Next: The order - Up: Appendix A: derivation WKB Previous: Appendix A: derivation WKB
Dr Yuri V Lvov 2007-01-23