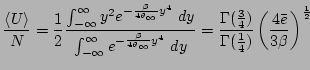Next: Bibliography
Up: Interactions of renormalized waves
Previous: Conclusions
Limiting behaviors of  for the thermalized
for the thermalized  -FPU chain
-FPU chain
We change variables
 in the
Hamiltonian (29) for
in the
Hamiltonian (29) for  -FPU to obtain
-FPU to obtain
![$\displaystyle H(p,y)=\sum_{j=1}^N\left[\frac{1}{2}p_j^2+\frac{1}{2}y_j^2+\frac{\beta}{4}y_j^4\right].$](img365.png) |
|
|
(74) |
Next, we compute the pdf's for the momentum and displacement.
Any  is distributed with the Gaussian pdf
is distributed with the Gaussian pdf
 and any
and any  is distributed with the
pdf
is distributed with the
pdf
 , where
, where  and
and
 are the normalizing constants. As we have discussed, the
renormalization factor
are the normalizing constants. As we have discussed, the
renormalization factor  of the
of the  -FPU system in thermal
equilibrium is given by Eq. (25), and its approximation via
the self-consistency argument
-FPU system in thermal
equilibrium is given by Eq. (25), and its approximation via
the self-consistency argument  is given by
Eq. (52). Here, we compare the behavior of both formulas
in two limiting cases, i.e., the case of small nonlinearity
is given by
Eq. (52). Here, we compare the behavior of both formulas
in two limiting cases, i.e., the case of small nonlinearity
 and the case of strong nonlinearity
and the case of strong nonlinearity
 . We will use the following expressions for
the average density of kinetic, quadratic potential and quartic
potential parts of the total energy of the system
. We will use the following expressions for
the average density of kinetic, quadratic potential and quartic
potential parts of the total energy of the system
In a
canonical ensemble, the temperature of a system is given by the
temperature of the heat bath. By identifying the average energy
density of the system with
 in our simulation (a
microcanonical ensemble), we can determine
in our simulation (a
microcanonical ensemble), we can determine  as a function of
as a function of
 and
and  by the following equation
by the following equation
 |
|
|
(78) |
We start with
the case of small nonlinearity
 . Suppose in the
first order of the small parameter
. Suppose in the
first order of the small parameter  the temperature has the
following form
the temperature has the
following form
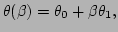 |
|
|
(79) |
where
 and
and
 . We find the values of
. We find the values of  and
and
 using the constraint (A5). We use the following
expansions in the small parameter
using the constraint (A5). We use the following
expansions in the small parameter 
| |
|
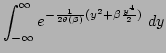 |
|
| |
|
 |
(80) |
| |
|
 |
|
| |
|
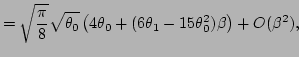 |
(81) |
| |
|
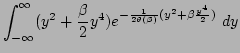 |
|
| |
|
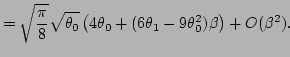 |
(82) |
Then, in the first order in  , Eq. (A5)
becomes
, Eq. (A5)
becomes
and we obtain
 and
and
 . Therefore, for
the average kinetic energy density, we have
. Therefore, for
the average kinetic energy density, we have
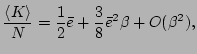 |
|
|
(83) |
and, for the average quadratic potential energy density, we
have
Finally, we obtain Eq. (53), i.e., for small

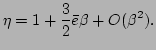 |
|
|
(85) |
Similarly, from Eq. (52), we find the small  limit
of the approximation
limit
of the approximation 
Now, we
consider the case of strong nonlinearity
 .
From Eq. (A5), we conclude that temperature in the large
.
From Eq. (A5), we conclude that temperature in the large
 limit, which we denote as
limit, which we denote as
 , stays bounded, i.e.,
, stays bounded, i.e.,
 and, in the limit of large
and, in the limit of large  , we obtain for
Eq. (A5)
, we obtain for
Eq. (A5)
 |
|
|
(86) |
After performing the integration, we obtain
 and the average kinetic energy density becomes
and the average kinetic energy density becomes
 . For the average quadratic potential energy
density, we have
. For the average quadratic potential energy
density, we have
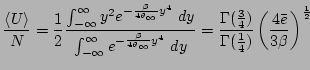 |
|
|
(87) |
For the renormalization factor, we obtain the following large
 scaling
scaling
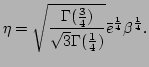 |
|
|
(88) |
Similarly, for the approximation of  , we obtain
, we obtain
 ,
,
 , and
, and
 . Therefore, the large
. Therefore, the large  scaling of
scaling of  becomes
becomes
 |
|
|
(89) |
which yields Eq. (54).



Next: Bibliography
Up: Interactions of renormalized waves
Previous: Conclusions
Dr Yuri V Lvov
2007-04-11