


Next: Resonant interaction in discrete
Up: Theoretical WT predictions
Previous: Preservation of the RPA
Steady power-law solutions of WKE which correspond to
a direct cascade of energy and an inverse waveaction cascade are,
where  and
and  are the energy and the waveaction fluxes
respectively and
are the energy and the waveaction fluxes
respectively and  and
and  are constants, and
are constants, and
 .
The first of these solutions is the famous ZF spectrum [8]
and it has a great relevance to the small-scale part of the sea
surface turbulence. It has been confirmed in a number of recent
numerical works [1,2,3], but we will also confirm it
in our simulation.
.
The first of these solutions is the famous ZF spectrum [8]
and it has a great relevance to the small-scale part of the sea
surface turbulence. It has been confirmed in a number of recent
numerical works [1,2,3], but we will also confirm it
in our simulation.
Now, let us consider the steady state solutions for the one-mode PDF.
Note that in the steady state
 which follows from
WKE (20). Then, the general steady state solution to (14)
is
which follows from
WKE (20). Then, the general steady state solution to (14)
is
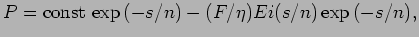 |
(27) |
where  is the integral exponential function.
At the tail
is the integral exponential function.
At the tail  we have
we have
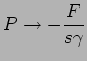 |
(28) |
if  . The
. The  tail decays much slower than the exponential
(Rayleigh) part and, therefore, it describes strong intermittency. On
the other hand,
tail decays much slower than the exponential
(Rayleigh) part and, therefore, it describes strong intermittency. On
the other hand,  tail cannot be infinitely long because otherwise
the PDF would not be normalizable. As it was argued in [5],
the
tail cannot be infinitely long because otherwise
the PDF would not be normalizable. As it was argued in [5],
the  tail should with a cutoff because the WT description breaks
down at large amplitudes
tail should with a cutoff because the WT description breaks
down at large amplitudes  . This cutoff can be viewed as a
wavebreaking process which does not allow wave amplitudes to exceed
their critical value,
. This cutoff can be viewed as a
wavebreaking process which does not allow wave amplitudes to exceed
their critical value,  for
for
 .
.
Relation between intermittency and a finite flux in the amplitude
space was observed numerically also for the Majda-Mc-Laughlin-Tabak
model by Rumpf and Biven [22].



Next: Resonant interaction in discrete
Up: Theoretical WT predictions
Previous: Preservation of the RPA
Dr Yuri V Lvov
2007-01-16
![]() which follows from
WKE (20). Then, the general steady state solution to (14)
is
which follows from
WKE (20). Then, the general steady state solution to (14)
is