Scaling Predictions

A renormalized WT theory derived in [#!prk:awttf!#] predicts that significant three wave interaction should occur in a band

$$\vert k\vert \le k_{\mathrm{knee}} \sim N \sqrt{\epsilon}$$ (9)

on a time scale

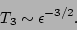$$T_{3} \sim \epsilon^{-3/2}.$$ (10)

This theory only applies when the lattice size is large enough ( $N \gg \epsilon^{-1/2}$) and the number of initially excited modes is an order unity fraction of the knee width $k_{\mathrm{knee}}$, so that the renormalized energy spectrum remains self-consistently of order unity during this phase of evolution.

A useful statistical measure for our purposes is the spectral entropy, defined as

$$S (t) = -\sum_k \frac{E_{h,k}(t)}{E_h(t)} \log\left(\frac{E_{h,k}(t)}{E_h(t)}\right).$$

This provides a measure of the effective number of excited normal modes at any given time, $n_{\mathrm{eff}}(t) \equiv e^{S(t)}$ [#!lc:fpupr!#,#!jdl:ueeoc!#,#!rl:etnlh!#,#!vvm:cbfce!#,#!pp:swtsr!#]. Figure 3 shows rescaled plots of this spectral entropy as a function of time. The onset of the quasi-stationary phase, after the end of the three-wave evolution, is clearly evident. The knee width $k_{\mathrm{knee}} \approx 1.5 N \sqrt{\epsilon}$ is determined as an average of $n_{\mathrm{eff}}$ over a time window shortly after the entropy ends its rapid rise. This scaling relationship is robust against various choices of initial bandwidth excitations. The time to reach partial equipartition $T_3$, however, does depend sensitively on the choice of initial data. As discussed above, the WT theory producing the scaling prediction (10) assumes the initial data is excited over a band of wavenumbers which is an order unity fraction of the knee width. To test the prediction (10), then, we choose the system to have initially $\frac{1}{2} k_{\mathrm{knee}}\approx 0.75 N \sqrt{\epsilon}$ excited modes. (The evolution depicted in Figure 1 comes from initial data of this form, whereas the example in Figure 2 was initialized with a considerably smaller band of excited modes). The time scale $T_3$ for the system to reach partial equipartition is determined automatically as the first time at which $n_{\mathrm{eff}}(t)$ achieves the value $k_{\mathrm{knee}}= 1.5 N \sqrt{\epsilon}$.