


Next: Setting the stage II:
Up: Setting the stage I:
Previous: Three-wave case
Consider a weakly nonlinear wavefield dominated by the 4-wave interactions, e.g.
the water-surface gravity waves [1,6,29,28],
Langmuir waves in plasmas [1,3] and the waves described by the
nonlinear Schroedinger equation [7].
The a Hamiltonian is given by (in the appropriately chosen variables)
as
As in three-wave case the most convenient form of equation of motion
is obtained in interaction representation,
 ,
so that
,
so that
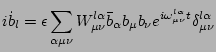 |
(11) |
where
 is an interaction coefficient,
is an interaction coefficient,
 .
We are going expand
in
.
We are going expand
in  and consider the long-time behaviour of a wave field, but
it will turn out that to do the perturbative expansion in a self-consistent
manner we have to renormalise
the frequency of (14) as
and consider the long-time behaviour of a wave field, but
it will turn out that to do the perturbative expansion in a self-consistent
manner we have to renormalise
the frequency of (14) as
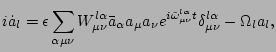 |
(12) |
where
 ,
,
 , and
, and
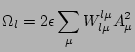 |
(13) |
is the nonlinear frequency shift
arising from self-interactions.



Next: Setting the stage II:
Up: Setting the stage I:
Previous: Three-wave case
Dr Yuri V Lvov
2007-01-23
