


Next: The case of nearly-diagonal
Up: Canonical Hamiltonians for waves
Previous: Four-wave case.
Preliminaries
In this Section, we set up the stage for formulation of our results.
Here, we give basic definitions, and obtain frequently used formulas.
We use the following definition of direct and inverse Fourier transforms:
Next, we generalize the Fourier transform to spatially inhomogeneous
systems. In order to do that, we
use a window transform of
 :
:
![$\displaystyle \Gamma[g(\textbf{x})]\equiv\tilde{g}(\textbf{x},\textbf{k}) = \fr...
...extbf{x}_0\vert)g(\textbf{x}_0)e^{-i\textbf{k}\cdot\textbf{x}_0}~d\textbf{x}_0.$](img79.png) |
|
|
(15) |
Here,  is an arbitrary fast decaying at infinity window
function. The parameter
is an arbitrary fast decaying at infinity window
function. The parameter
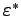 is defined by the spatial scales of
the inhomogeneity and the propagating wave-packets in the following manner. First, we introduce
the characteristic length of inhomogeneity to be of the order
is defined by the spatial scales of
the inhomogeneity and the propagating wave-packets in the following manner. First, we introduce
the characteristic length of inhomogeneity to be of the order
 . Then, we take the width of the window, which is of the order
. Then, we take the width of the window, which is of the order
 , to be much smaller than the characteristic length of
inhomogeneity. On the other hand, the width of the window is chosen
to be much larger than the wavelength of the waves that propagate in
the inhomogeneous medium, which is of the order
, to be much smaller than the characteristic length of
inhomogeneity. On the other hand, the width of the window is chosen
to be much larger than the wavelength of the waves that propagate in
the inhomogeneous medium, which is of the order  . Therefore, we
have
. Therefore, we
have
 |
|
|
(16) |
The special case when
 is called Gabor
transform [17]. Note that, when
is called Gabor
transform [17]. Note that, when
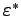 approaches zero,
approaches zero,
 approaches the constant function with the value
one. Consequently, the Gabor transform becomes a Fourier transform.
Therefore the Fourier transform can be seen as an averaging over an
infinitely large window.
approaches the constant function with the value
one. Consequently, the Gabor transform becomes a Fourier transform.
Therefore the Fourier transform can be seen as an averaging over an
infinitely large window.
The inverse of the window transform (17) is given by
 |
|
|
(17) |
where we have used  . We emphasize that
Eq. (19) and all the formulas that we obtain below
can be obtained using any fast decaying at infinity window function
and are independent of the particular form of
. We emphasize that
Eq. (19) and all the formulas that we obtain below
can be obtained using any fast decaying at infinity window function
and are independent of the particular form of  as long as it is
sufficiently smooth.
as long as it is
sufficiently smooth.
Now, we present the formulas for the window transform, which will be
useful later. First, we express the window transform
 in terms of the Fourier transform
in terms of the Fourier transform

 |
|
|
(18) |
Next, we express the Fourier image
 in terms of the window
variable
in terms of the window
variable

 |
|
|
(19) |
By combining Eqs. (20) and (21), we obtain
the following formula
 |
|
|
(20) |
After introducing notations and formulas that will be extensively used below, we proceed to the discussion of the main results of the paper.



Next: The case of nearly-diagonal
Up: Canonical Hamiltonians for waves
Previous: Four-wave case.
Dr Yuri V Lvov
2008-07-08




![]() in terms of the Fourier transform
in terms of the Fourier transform
![]()