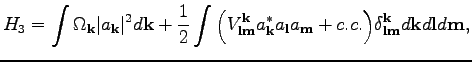Three-wave case.

The quadratic Hamiltonian of a three-wave system with small scale perturbations on the background of the large scale excitations is given by Eq. (4). In order to show that, we start with a standard three-wave Hamiltonian [10]:

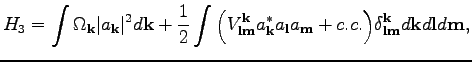$$H_3=\int\Omega _\textbf{k}\vert a_\textbf{k}\vert^2d\textbf{k}+\f... ...ig)\delta^\textbf{k}_{\textbf{l}\textbf{m}} d\textbf{k}d\textbf{l} d\textbf{m},$$ (6)

where $V$ is an interaction coefficient. Then, the equations of motion for the variable $a_\textbf{k}$ assume a standard form

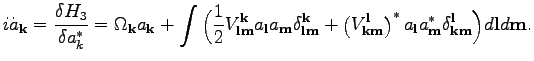$$i\dot{a}_\textbf{k}=\frac{\delta H_3}{\delta a_k^*} = \Omega _{\t... ...extbf{m}^*\delta^\textbf{l}_{\textbf{k}\textbf{m}}\Big) d\textbf{l}d\textbf{m}.$$ (7)

Suppose that a large-scale solution of (8) is given by $C_\textbf{k}$ . We consider a perturbed solution $a_\textbf{k}=C_\textbf{k}+c_\textbf{k}$ where $c_\textbf{k}$ is a small-scale perturbation of $C_k$ . Equation of motion for $c_\textbf{k}$ attains the following form:

$$i\dot{c}_\textbf{k}=\Omega _{\textbf{k}}c_{\textbf{k}}+\int \left... ...f{m}^*)\delta^\textbf{l}_{\textbf{k}\textbf{m}} \right] d\textbf{l}d\textbf{m}.$$

Now, we use the fact that $C_\textbf{k}$ is a known exact solution for Eq. (9) to obtain

$$i\dot{c}_\textbf{k}=\int A(\textbf{k},\textbf{l})c_\textbf{l}d\te... ...f{m}^* \delta^\textbf{l}_{\textbf{k}\textbf{m}} \right] d\textbf{l}d\textbf{m},$$ (8)

where

$$A(\textbf{k},\textbf{l}) = \Omega _\textbf{l}\delta_\textbf{l}^\textbf{k}+V^\textbf{k}_{\tex... ...xtbf{l}_{\textbf{k},\textbf{l}-\textbf{k}}\right)^*C^*_{\textbf{l}-\textbf{k}},$$ (9)

$$B(\textbf{k},\textbf{l}) = 2V^{\textbf{k}-\textbf{l}}_{\textbf{k},-\textbf{l}}C_{\textbf{k}-\textbf{l}}.$$

Equation (9) corresponds to the following Hamiltonian

$$H=\int A(\textbf{k},\textbf{l})c_\textbf{l}c_\textbf{k}^*d\textbf... ...delta^\textbf{k}_{\textbf{l}\textbf{m}}+c.c.]d\textbf{k}d\textbf{l}d\textbf{m}.$$ (10)

This appears to be a standard form of the Hamiltonian for the wave system dominated by three wave interactions in the inhomogeneous media. Quadratic in $c_\textbf{k}$ part of this Hamiltonian is given by (4), while cubic part of this Hamiltonian is a standard three-wave interaction Hamiltonian.