


Next: Statistical averaging and graphs.
Up: Evolution of the multi-mode
Previous: Generating functional.
Let us first obtain an asymptotic weak-nonlinearity expansion
for the generating functional
 exploiting the separation of the linear and
nonlinear time scales. 2 To
do this, we have to calculate
exploiting the separation of the linear and
nonlinear time scales. 2 To
do this, we have to calculate  at the intermediate time
at the intermediate time  via
substituting into it
via
substituting into it  from (8)
and retaining the terms up to
from (8)
and retaining the terms up to
 only.
This calculation is given in the Appendix and the result of it is:
only.
This calculation is given in the Appendix and the result of it is:
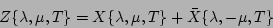 |
(16) |
with
![\begin{displaymath}
X\{\lambda, \mu,T\} = X(0) + (2 \pi)^{2N} \left<\prod_{\Vert...
...+{\epsilon}^2(J_2 +J_3+J_4+J_5)] \right>_A + O({\epsilon}^4),
\end{displaymath}](img113.png) |
(17) |
where
where
 and
and
 denote
the averaging over the initial amplitudes and initial phases
(which can be done independently).
Our next step will be to calculate the above terms by substituting
into them the values of
denote
the averaging over the initial amplitudes and initial phases
(which can be done independently).
Our next step will be to calculate the above terms by substituting
into them the values of  and
and  from (9)
and (10) respectively.
from (9)
and (10) respectively.



Next: Statistical averaging and graphs.
Up: Evolution of the multi-mode
Previous: Generating functional.
Dr Yuri V Lvov
2007-01-17
![]() exploiting the separation of the linear and
nonlinear time scales. 2 To
do this, we have to calculate
exploiting the separation of the linear and
nonlinear time scales. 2 To
do this, we have to calculate ![]() at the intermediate time
at the intermediate time ![]() via
substituting into it
via
substituting into it ![]() from (8)
and retaining the terms up to
from (8)
and retaining the terms up to
![]() only.
This calculation is given in the Appendix and the result of it is:
only.
This calculation is given in the Appendix and the result of it is: