


Next: Appendix 2
Up: Joint statistics of amplitudes
Previous: Discussion
Let us obtain  in terms of the series in small nonlinearity
up to the second order in
in terms of the series in small nonlinearity
up to the second order in  .
As an intermediate step, we first consider
separately the amplitude and the phase ingredients of
.
As an intermediate step, we first consider
separately the amplitude and the phase ingredients of  and
substitute the
and
substitute the  -expansion of
-expansion of  from (8) into
their expressions,
from (8) into
their expressions,
and
where
 and
and  denote the
linear and quadratic contributions into the amplitude and phase parts of
denote the
linear and quadratic contributions into the amplitude and phase parts of  respectively,
respectively,
Substituting expansions (64) and (65) into the
expression for  , we have
, we have
For parts  and
and
 in the above expression we have,
in the above expression we have,
Exploiting the
property
 we can write
we can write
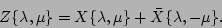 |
(69) |
At  we have for
we have for

![\begin{displaymath}
X(T) = X(0) + (2 \pi)^{2N} \left<\prod_{\Vert l\Vert<N}
e^{...
...^2}[{\epsilon}J_1 +{\epsilon}^2(J_2 +J_3+J_4+J_5)] \right>_A,
\end{displaymath}](img429.png) |
(70) |
where
where
 and
and
 denote
the averaging over the initial amplitudes and initial phases
respectively. We remind that such individual averages are possible
because the amplitudes and the phases are statistically independent
from each other at
denote
the averaging over the initial amplitudes and initial phases
respectively. We remind that such individual averages are possible
because the amplitudes and the phases are statistically independent
from each other at  .
.



Next: Appendix 2
Up: Joint statistics of amplitudes
Previous: Discussion
Dr Yuri V Lvov
2007-01-17
![]() in terms of the series in small nonlinearity
up to the second order in
in terms of the series in small nonlinearity
up to the second order in ![]() .
As an intermediate step, we first consider
separately the amplitude and the phase ingredients of
.
As an intermediate step, we first consider
separately the amplitude and the phase ingredients of ![]() and
substitute the
and
substitute the ![]() -expansion of
-expansion of ![]() from (8) into
their expressions,
from (8) into
their expressions,


![$\displaystyle \frac{\mu_j}{2A_j^{(0)2}}(a_j^{(2)}\bar
a_j^{(0)}-\bar a_j^{(2)}a...
...
a_j^{(0)}}\right)^2
\right]-\frac{\mu_j^2\vert a_j^{(1)}\vert^2}{4A_j^{(0)2}}.$](img411.png)


}a_j^{(0)})^2,$](img422.png)

![]() we can write
we can write