


Next: Discussion
Up: Probability densities and preservation
Previous: In what sense are
We have established above that
the one-point statistics are at the heart of WT theory.
All one-point statistical objects can be derived from the one-point
amplitude generating function,
which can be
obtained from the  -point
-point  by taking all
by taking all  's and all
's and all
 's, except for
's, except for  , equal to zero. Substituting such
values into (15) we get the following equation for
, equal to zero. Substituting such
values into (15) we get the following equation for  ,
,
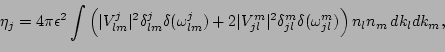 |
(21) |
where,
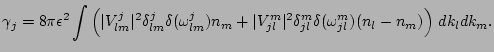 |
|
|
(22) |
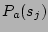 |
|
|
(23) |
Correspondingly, for the one particle PDF  we have
we have
 |
(24) |
with  is a probability flux in the s-space,
is a probability flux in the s-space,
 |
(25) |
Equations (22) and (25) where previously obtained and
studied in [21] in for four-wave systems. The only
difference for the four-wave case was different expressions for  and
and  . For the three-wave case, the equation for the PDF was not
considered before, but equations for its moments were derived and
solved in [19]. In particular, the equation for the first moment is
nothing but the familiar kinetic equation
. For the three-wave case, the equation for the PDF was not
considered before, but equations for its moments were derived and
solved in [19]. In particular, the equation for the first moment is
nothing but the familiar kinetic equation
 which gives
which gives
 for any steady state. This, in turn
means that in the steady state with
for any steady state. This, in turn
means that in the steady state with  we have
we have
 where
where  can be any steady state solution
of th kinetic equation including the KZ spectrum which plays the
central role in WT [2,17]. However, it was shown in
[21] that there also exist solutions with
can be any steady state solution
of th kinetic equation including the KZ spectrum which plays the
central role in WT [2,17]. However, it was shown in
[21] that there also exist solutions with  which
describe WT intermittency.
which
describe WT intermittency.



Next: Discussion
Up: Probability densities and preservation
Previous: In what sense are
Dr Yuri V Lvov
2007-01-17