


Next: Evolution of the Generating
Up: Probability densities and preservation
Previous: Definition of an essentially
Consider weakly nonlinear dispersive waves in a periodic box with a
dispersion relation  which allow three-wave
interactions. Example of such systems include surface capillary
waves [2,], Rossby waves [9] and
internal waves in the ocean [8]. In Fourier space, we have the
following Hamiltonian equations,
which allow three-wave
interactions. Example of such systems include surface capillary
waves [2,], Rossby waves [9] and
internal waves in the ocean [8]. In Fourier space, we have the
following Hamiltonian equations,
where  is the complex wave amplitude in the interaction
representation,
is the complex wave amplitude in the interaction
representation,
 is the wavevector,
is the wavevector,  is the box
side length,
is the box
side length,
 ,
,
 is the wave frequency,
is the wave frequency,
 is a
formal nonlinearity parameter. Here, the interaction coefficient
is a
formal nonlinearity parameter. Here, the interaction coefficient
 is obviously symmetric with respect to
is obviously symmetric with respect to  and
and  but we
do not assume any further symmetries.2
but we
do not assume any further symmetries.2
In order to filter out fast oscillations at the wave period, let us
seek for the solution at time  such that
such that
 . The second condition ensures that
. The second condition ensures that  is a lot
less than the nonlinear evolution time. Now let us use a perturbation
expansion in small
is a lot
less than the nonlinear evolution time. Now let us use a perturbation
expansion in small  ,
,
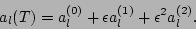 |
(12) |
Substituting this expansion in (11) we get in the
zeroth order
 ,
i.e. the zeroth order term is time independent. This corresponds to
the fact that in the interaction representation, wave amplitudes are
constant in the linear approximation. For simplicity, we will write
,
i.e. the zeroth order term is time independent. This corresponds to
the fact that in the interaction representation, wave amplitudes are
constant in the linear approximation. For simplicity, we will write
 , understanding that a quantity is taken at
, understanding that a quantity is taken at  if its time argument is not mentioned explicitly. The first order is
given by
if its time argument is not mentioned explicitly. The first order is
given by
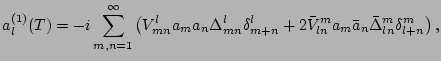 |
|
|
(13) |
where
 Iterating one more time we get
Iterating one more time we get
where we introduced




Next: Evolution of the Generating
Up: Probability densities and preservation
Previous: Definition of an essentially
Dr Yuri V Lvov
2007-01-17
![]() which allow three-wave
interactions. Example of such systems include surface capillary
waves [2,], Rossby waves [9] and
internal waves in the ocean [8]. In Fourier space, we have the
following Hamiltonian equations,
which allow three-wave
interactions. Example of such systems include surface capillary
waves [2,], Rossby waves [9] and
internal waves in the ocean [8]. In Fourier space, we have the
following Hamiltonian equations,
![]() such that
such that
![]() . The second condition ensures that
. The second condition ensures that ![]() is a lot
less than the nonlinear evolution time. Now let us use a perturbation
expansion in small
is a lot
less than the nonlinear evolution time. Now let us use a perturbation
expansion in small ![]() ,
,
![]()