next up previous
Next: Nonlinear, Non-Rotating Shallow Waters Up: Hamiltonian formalism for long Previous: Hamiltonian formalism for long

Linear, Non-Rotating Shallow Waters

In non-dimensional form, the shallow-water equations take the form

$\displaystyle h_t + \nabla \cdot (h \vec u)$ $\textstyle =$ $\displaystyle 0,$ (1)
$\displaystyle {\vec u}_t + (\vec u \cdot \nabla) \vec u + \nabla h$ $\textstyle =$ $\displaystyle 0\, .$ (2)

Here $h$ represents the height of the free-surface, and $\vec{u}$ the horizontal velocity field. The height $h$ has been normalized by its mean value $H$, the velocity field $u$ by the characteristic speed $c = \sqrt{g h}$ (here $g$ is the gravity constant), the horizontal coordinates by a typical wavelength $L$, and time by $L/c$. Writing

\begin{displaymath}h = 1 + \eta \, , \end{displaymath}

and assuming that $\eta$ and $\vert u\vert$ are much smaller than one, one obtains to leading order the linearized equations
$\displaystyle \eta_t + \nabla \cdot \vec u$ $\textstyle =$ $\displaystyle 0,$ (3)
$\displaystyle \vec u_t + \nabla \eta$ $\textstyle =$ $\displaystyle 0\, .$ (4)

At this linear level, the dynamics of waves and vorticity decouple, with the former satisfying the wave equation, and the latter remaining constant in time. In particular, if the flow is initially irrotational (i.e., $\nabla \times \vec u = 0$), it will remain so forever. Hence we may restrict our attention here to irrotational flows. These may be described by a scalar potential $\phi$, such that

\begin{displaymath} \vec u = \nabla \phi \, . \end{displaymath}

For such flows, the system in ([*], [*]) reduces to
$\displaystyle \eta_t + \Delta \phi$ $\textstyle =$ $\displaystyle 0\, ,$  
$\displaystyle \phi_t + \eta$ $\textstyle =$ $\displaystyle 0.$  

This system is Hamiltonian, with
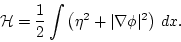\begin{displaymath} {\cal H}= \frac{1}{2} \int \left(\eta^2 + \vert\nabla\phi\vert^2 \right) \, dx . \end{displaymath} (5)

The Hamiltonian form of the equations is
$\displaystyle \eta_t$ $\textstyle =$ $\displaystyle \frac{\delta {\cal H}}{\delta \phi} \, ,$ (6)
$\displaystyle \phi_t$ $\textstyle =$ $\displaystyle - \frac{\delta {\cal H}}{\delta \eta} \, .$ (7)

Notice that the Hamiltonian in ([*]) is the sum of the potential and kinetic energy of the system. The former is actually given by $\frac{1}{2} (1+\eta)^2$, but the difference can be absorbed by a gauge transformation of the potential $\phi$. Our goal is to preserve the essential simplicity of this formulation when we add nonlinearity, ambient rotation, stratification and vertical shear.

next up previous
Next: Nonlinear, Non-Rotating Shallow Waters Up: Hamiltonian formalism for long Previous: Hamiltonian formalism for long
Dr Yuri V Lvov 2007-01-17